Roofline模型非常简洁,却对计算加速有很好的指导意义。它要解决的是“计算量为$N$且访存量为$V$的算法,在算力为$P_{peak}$且带宽为$B$的计算平台所能达到的理论性能上限是多少”这个问题。可以帮助分析当前算法的性能是受算法实现所限还是平台本身算力限制,进而更有针对性地改进算法性能。
Roofline模型
给定一个计算平台,它的峰值算力\(P_{peak}\)(单位flop/s),带宽\(B\)(单位byte/s)。
给定一个算法,它的计算量为\(N\)(单位flop),访存量为\(V\)(单位byte),定义计算强度\(I\)(computational intensity,计算访存比,单位flop/byte)
则该算法的理论性能\(P\)上限为
\[P = min(P_{peak}, IB)\]注:\(P\)代表算法每秒浮点运算次数,即使用的算力,不等同于算法执行时间。比如这里举的例子:单从\(P\)来说,VGG是MobileNet的3倍(且VGG处于Compute limited区域,MobileNet处于Memory limited区域),但是MobileNet的总计算量是VGG的三十分之一,因此MobileNet的计算时间是VGG的十分之一(理论值)。
绘制算法性能\(P\)和算法计算强度\(I\)的曲线,如下图红色实线所示
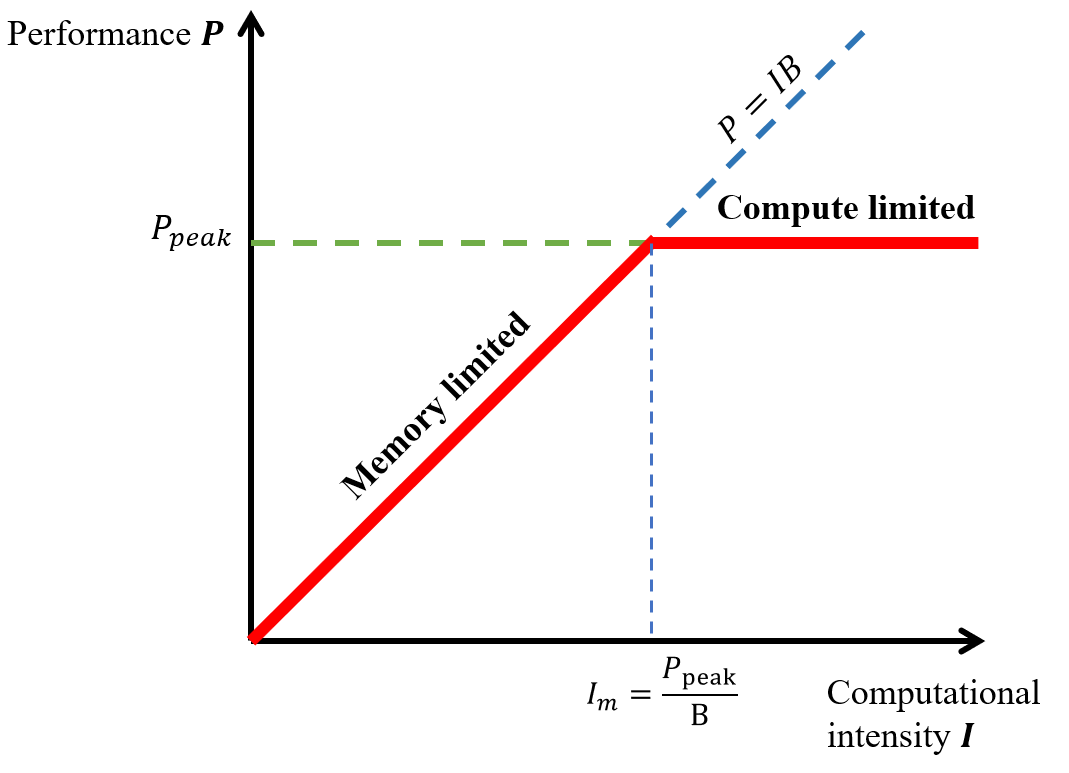
可以看到,在Roofline模型中,算法的性能由\(P_{peak}\),\(B\)和\(I\)三个变量决定。前面二者是硬件本身的参数,因此编码时主要可以考虑从\(I\)出发,改善性能。
计算强度\(I\)可以形象地体现编写的代码质量。
- 当\(I \ge \frac{P_{peak}}{B}\)时,处于
compute limited区域,此时所使用的算力达到硬件峰值,算力充分利用;- 要进一步提升性能,则需要提升硬件本身峰值算力。
- 当\(I < \frac{P_{peak}}{B}\)时,处于
Memory limited区域,算法执行受到访存限制(访存过多或利用率较低)。- 此时需要提升计算强度,比如:
- 算子融合,则是在相同计算量的情况下,避免了中间的访存过程,从而降低了访存量,提升计算强度;
- 矩阵乘法中,通过合理的分块等方式,减低访存量,增大计算强度。
- 此时需要提升计算强度,比如:
举例
比如给定计算平台峰值算力\(P_{peak} = 4\ GFlop/s\),带宽\(B = 10\ GByte/s\)
下面一个小demo
1
2
3
4
float a[N], b[N], c[N];
for (int i = 0; i < N; ++i) {
c[i] = a[i] + b[i];
}
每个循环进行了2次浮点运算(2 flop),产生12 byte的访存(3 * 4 byte/float),故计算强度为\(\frac{1}{6}\) flop/byte < \(\frac{P_{peak}}{B} = \frac{2}{5}\) flop/byte,故处于memory limited区域,需要进一步提升计算强度以提升性能。